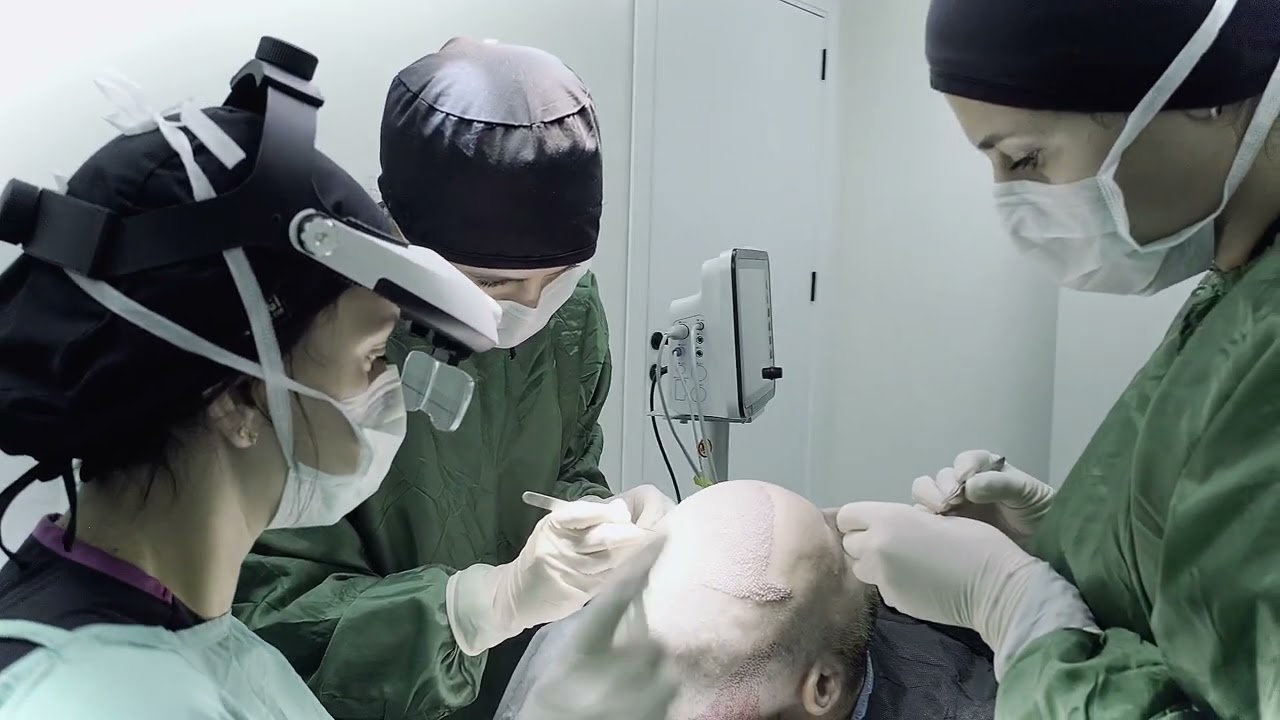
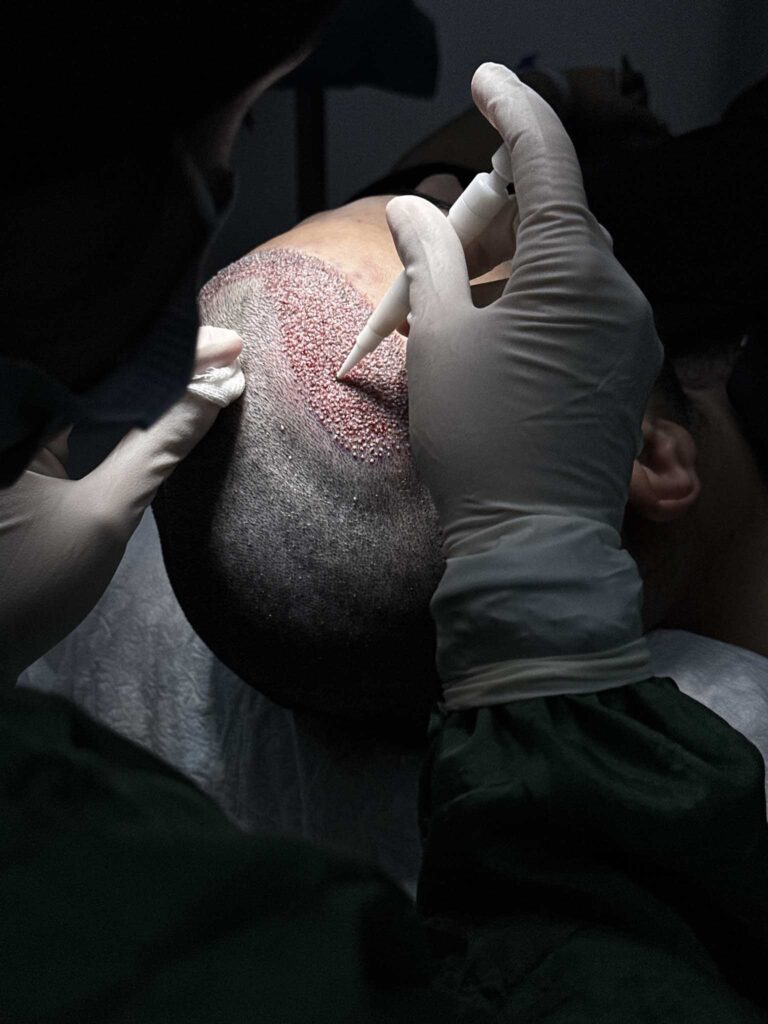
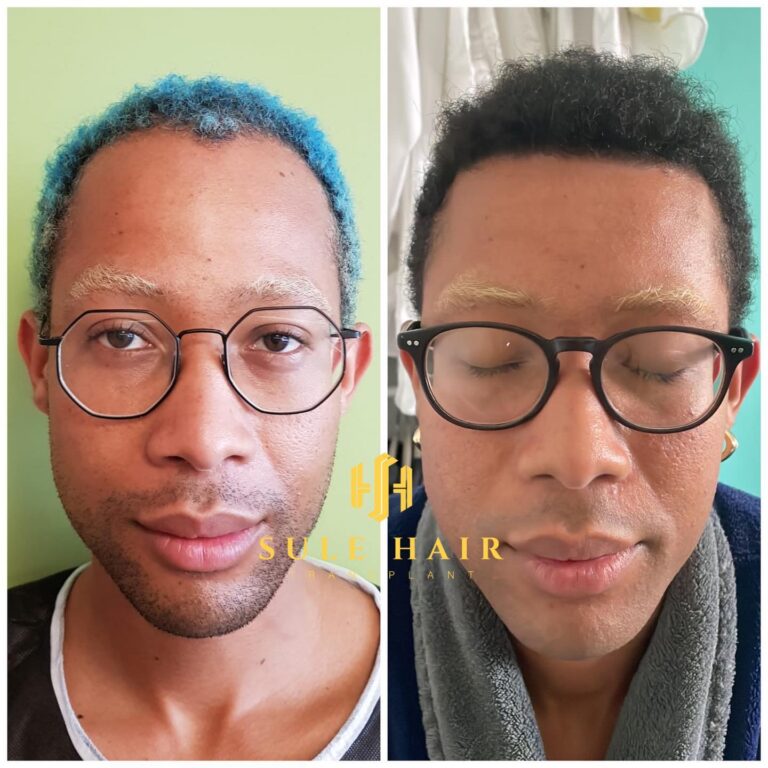
Quem é elegível para um transplante capilar na Turquia?
Para ser elegível para um transplante capilar na Turquia, é necessário satisfazer critérios específicos. Os principais factores que determinam a elegibilidade incluem
- Queda de cabelo permanente: Deve ter uma queda de cabelo irreversível, o que significa que não se espera que a sua queda de cabelo reverta ou volte a crescer naturalmente.
- Estabilidade da queda de cabelo: A sua queda de cabelo deve ter atingido um ponto estável, indicando que não está a piorar progressivamente.
- Ausência de doenças transmissíveis pelo sangue: É essencial que não sofra de nenhuma doença transmitida pelo sangue que possa complicar o procedimento ou colocar em risco a sua saúde ou a de outros.
- Sem historial de má cicatrização de feridas: Se tiver um historial de cicatrização lenta ou problemática de feridas, isso pode afetar o sucesso da cirurgia de transplante capilar.
- Boa saúde geral: É fundamental manter um bom estado de saúde geral. Isto assegura que pode tolerar bem o procedimento e que tem mais hipóteses de obter um resultado positivo.
Em resumo, a elegibilidade para um transplante capilar na Turquia depende da existência de uma queda de cabelo permanente que tenha estabilizado, de não ter doenças transmitidas pelo sangue, de não ter historial de má cicatrização de feridas e de manter uma boa saúde geral.